Module 17 Project

Introduction

In this PA you will implement some analysis routines over a data structure called an expression tree. You will implement similar projects in Ruby, Haskell, and Prolog, and the goal is to explore the differences between the three languages.

In Ruby, you will extend existing Ruby classes to practice dynamic object-oriented programming. In Haskell, you will write pattern-matching routines to practice functional programming. In Prolog, you will write rules to practice logical programming.

Project starter files: p6.zip

Requirements

This version of the project does not have a lexer and parser. There is a way to generate parsers in Prolog called definite clause grammars but they are not as easy to use as the lexer and parser generators for Ruby and Haskell. Thus, you will need to create test cases manually. A few have been provided in test.pl for your reference.

In Prolog, we choose to represent expression trees using recursive lists. This definition allows us to match pattern in a way that is similar to Haskell. However, one major difference between Haskell and Prolog is that Haskell is strongly typed but Prolog is not. In particular, Prolog lists can store items of differing types, and will will take advantage of this in our representation.

We define an expression tree as a list that has one of the following symbols as its head: eint, eadd, esub, emul. You will note that these are nearly identical to the value constructors from Haskell, except that they must begin with a lower-case letter because identifiers that start with upper-case letters are variables in Prolog. The remainder of the list contains either the integer value (for eint) or two subtrees in the form of sublists (for eadd, esub, or emul).

For instance, the expression (2+3)*4 is equivalent to the following tree:

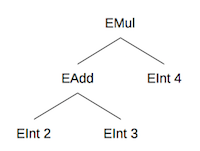
Here is the corresponding representation in Prolog:

[emul,[eadd,[eint,2],[eint,3]],[eint,4]]

Your task in this PA will be to write various predicates to analyze expression trees. You will do this by writing predicates that define the values of various properties of an expression tree.

Unlike in Haskell, you won’t necessarily need to handle every node type separately in Prolog because the node type symbols (eint, eadd, etc.) are just symbols and not value constructors. This means you can use _ (the anonymous variable, like in Haskell) to match any node type.

Below are descriptions of the functions you need to implement. You can also look at the test cases (in test.pl) to see what they are supposed to do.

• eval(T,X) - Calculates the result of evaluating the mathematical expression. All operations should be done using integer arithmetic. Read as “the result of evaluating expression tree T is X.”
• countOps(T,X) - Counts the total number of arithmetic operations in an expression. All three operations (addition, subtraction, and multiplication) count for this process. Read as “the number of operations in expression tree T is X.”
• height(T,X) - Calculates the height of the expression tree, where the height of a single-node tree is defined as being 1. Read as “the height of expression tree T is X.”
• postfix(T,X) - Builds a flattened postfix list representation. For example, (2+3)*4 in postfix notation would be [2,3,+,4,*] (note that all of the operator symbols are atoms in Prolog). Read as “the postfix representation of T is X.”
• uniqInts(T,X) - Extract a sorted list of all unique integers in an expression. Each integer should appear in the resulting list only once. Read as “the list X is a sorted list of all the unique integers in expression tree T.”

For the last function (uniqInts), you may find it helpful to write a helper predicate:

• uniq(L,M) - Remove duplicates from a list. Read as “the list M is equivalent to list L with all duplicates removed.”

You may also find the Prolog built-in sort predicate useful.

Some test routines are included in test.pl. However, your submission will be graded based on additional tests not provided to you, so you should write your own test cases as well.

There is no expression parser in Prolog for this project, so you’ll need to hard-code the expression trees in your test cases. Here is some code that you can add to your P2 (Ruby) solution to generate inputs for P6 (Prolog)–note that you can add new cases by adding them to the array:

class EInt; def to_p6; "[eint,#{@val.to_s}]"                 end end
class EAdd; def to_p6; "[eadd,#{left.to_p6},#{right.to_p6}]" end end
class ESub; def to_p6; "[esub,#{left.to_p6},#{right.to_p6}]" end end
class EMul; def to_p6; "[emul,#{left.to_p6},#{right.to_p6}]" end end

if __FILE__ == $0
  ["1", "1+2", "5-3", "2*4", "1+2*3"].each do |e|
    expr = parse_expr(e)
    puts "#{expr.to_s} => #{expr.to_p6}"
  end
end

For this assignment, you may NOT use any classes or methods that are not in the base Prolog language. Your submission will be graded using SWI-Prolog 7.6.4 and so it must run correctly using that version. You may use other versions of Prolog for development if you wish, but you should test with SWI-Prolog 7.6.4 before you submit to make sure you aren’t using any features that are specific to a different implementation or version.

Submission

Your program must contain implementations as described above. You must name your Prolog script file p6.pl. You must put your name in a comment at the top of the file. As usual, decompose your methods to make them more readable, use good names, indent properly, and so on. You will partly be graded on the readability of your code but mostly on whether it works.

Submit ONLY p6.pl to the appropriate assignment on Canvas by the deadline.